FXの期待値|AIと検討するトレード手法|勝てない・・・期待値はあるのか・・・??

もう何年もトレードしているのに、TPもSLもLOTも決められない・・・勝てない!FXトレードにエッジ・期待値ってあるの?

結論、あなたの見つけたエッジに優位性はありません。
静的なルールに基づく戦略に、持続可能なエッジは存在しないのです。
AIを活用していると、何でもかんでもAIに聞いてみたくなってしまいます。彼らは明確に答えを出してくれますが、AIの回答は常にハルシネーションを疑い、あくまでも参考情報として活用するのが良いと思います。この記事も、それを前提に、ご参考ください。
なぜ私がエントリすると逆へ行くのか
私がエントリすると逆へ行く、この相場の動き・値動きは、ジグザグの波動を描いています。作っているインジケータを改良し、波動の大きさについて、知ってみようと思いました。そこから、何かトレードヒントを得られないか?波動の大きさはTPやSLに直結するものだし・・・
「波動の大きさ」に注目して、TPやSLを決められないか?あわよくば、エッジ・期待値のある手法に結びつかないか!?というところから、「波動の大きさの検討」がスタートしました。
まずは、自分の見ている波動の大きさを知る
FXの常識:「期待値」という唯一の羅針盤
トレードの世界には、数多くの「常識」があふれています。その中でも特に強力なのが「損小利大」という思想でしょう。
「fx ペイオフレシオ 勝率 期待値」の関係性:バルサラの破産確率が示す真実
まず、全てのトレーディング戦略の優劣を測る、唯一にして絶対の物差しを確認しましょう。それが「期待値」です。FXの期待値の計算式は、驚くほどシンプルです。
期待値 = (平均利益 × 勝率) – (平均損失 × 敗率)
この値がプラスであれば、そのトレードを繰り返すことで、長期的には資産が増えていくことを意味します。ここで重要なのが、ペイオフレシオ(リスクリワード)と勝率の関係です。
- 損小利大(RR > 1): 平均利益が平均損失を上回る戦略。勝率が50%以下でも、期待値をプラスにできる可能性がある。
- 損大利小(RR < 1): 平均利益が平均損失を下回る戦略。期待値をプラスにするには、非常に高い勝率が求められる。
バルサラの破産確率表は、この関係性を示し、「損大利小」がいかに危険な領域であるかを警告しています。バルサラの破産確率表は、高勝率であれば、生き延びることも示唆しています。
つまり、現実的な戦略は2通り。
- 高勝率 RR<1
- 低勝率 RR>1
高勝率 RR>1が良いのは言うまでもありませんが・・・こんなできたら苦労しない。とりあえず、わたしの性格的に、高勝率手法を検討したいと、思いました。
高勝率戦略の可能性:市場の「歪み」を利用
もし、市場の動きに統計的な偏りがあり、それを利用して高い勝率を実現できるとしたら?RRが1未満であっても、期待値をプラスにし、かつ安定した利益を達成できるのではないか。素人ならではの考えですが、難しい。
目指すのは、一発逆転のホームランではなく、確実にヒットを積み重ねる、高勝率な期待値が高い手法。ヒットとは言え、通常は、RR>1 勝率50%以上を維持することはMUSTだと思いますので、ご注意ください。
もし、FXの値動きの大きさ・波動の大きさが特徴的であれば・・・
「言うは易し」ですが、どうやって高勝率を実現するのか。値動きの「値動き・波動の大きさの分布」に注目してみました。
データが示す市場の姿:統計で探る「期待値の高い手法」
過去のデータセットを複数確認した結果、波動の大きさは「対数正規分布」という、特徴的な統計モデルに従う可能性が高いことが分かりました。ただしこれは、一般的に既知の概念です(非常に一般的)。ここまでは、わたくし自身でデータセットを確認したり・・・一般的な概念を、実データで再確認した形ですね。
では、これは、何を意味するのか?活用する方法は無いか?
ここから、AIの力も借りて、あーだこーだ考えてみることにしました。

このインジケータでは、データセットをテキスト出力できます。AIによっては、それをそのまま読み込んで解析できます。
ご自身が認識している波動の大きさがどの程度なのか?確認してみると面白いかもしれません。このインジケータなら、確認が容易です(そう、宣伝です!)。
値動き・波動の大きさが対数正規分布であるとすれば・・・
- 小さな波は、極めて頻繁に発生する。
- 大きな波は、ごく稀にしか発生しない。
- 代表値がズレる:
- 最頻値 (Mode): 最もよく出現する波の大きさ >>これが分布のピークになりますが、左にズレます
- 中央値 (Median): 全ての波を大きさ順に並べた真ん中の値
- 平均値 (Mean): 全ての波の平均的な大きさ
この対数正規分布の特徴は、値動きとして、とても実際的な感じがしました。たまーに、滅茶苦茶大きな波動が生じる。この「Mode < Median < Mean」という歪んだ構造は、市場の非効率性を示しているのかもしれません。分布は、右すそが長い構造で、右すそは滅茶苦茶伸びるときは伸びまくる。なるほど、教科書的な損小利大で勝率<50%のトレードは、まさにこの分布が示す通り、Tailを狙ったトレードなのでは。Tailを狙うか、分布の中腹を狙うか・・・
数学が導き出す結論:「RR<1」の優位性
そして、値動きの分布がこの統計モデルであるとすれば、「”RR<1″という戦略が、”RR=1近辺”を狙うよりも優位性が高い可能性がある※」「構造的エッジがある」と述べるAIが存在しました。
※注意点として、様々なAIは、「まずはRR>1 戦略」を当然おススメしてきます。
基本的にはRR>1戦略。
ただし、RR<1とする戦略も存在する。RR≒1よりも優位性があるかもしれない。
(必要勝率は確保した上で)
このRR<1戦略は、典型的な「損大利小」です。常識的に考えれば、地獄への片道切符に見えます。しかし、AIによっては、具体的な数値例として・・・
- RR 0.7
- このモデルにおける理論上の勝率(構造的エッジ): 約71%
であると述べ、理論的勝率:「構造的エッジ」が存在することを示唆していました。これは、「ランダムにエントリーしても、取引コストがゼロであって、かつ無限に試行を繰り返せば、期待値はプラスになる」という、あくまで理論上の話ではあるのですが。
ちなみに、私はこの「構造的エッジ」という言葉を少し信じてしまったところがあり、あまり深く考えずにエントリーしまくったことがあります。結果はもちろん、壊滅的な損失を被りました【参考記事】。この経験が教えてくれたのは、『構造的エッジ』とは、何もしなくても勝てる魔法ではなく、エントリー精度という人間の努力によって初めて利益に転換できる、微かな追い風に過ぎない、という厳しい現実でした(笑)
そりゃ当たり前すよねえ・・・

AIによる補足:なぜRR<1が合理的な選択肢となり得るのか
この対数正規分布という歪んだ分布においては、最も期待値が高くなるスイートスポットは、RR<1の領域に存在するケースもあると考えます。
これは、精神論ではありません。数学的な事実です。
- RR>1(Tailを狙う)戦略: 一般的なトレード手法・概念です。発生確率の低い「大きな波(Tail:分布の右すそ)」を追い求めるため、人によっては、精神的に過酷(低勝率となる)でしょう。
- RR≒1 戦略: 分布の最も特徴のない部分を狙うため、数学的には優位性が低くなりました。実トレードでは、この点は感じにくいでしょう。
- RR<1 戦略: 発生確率が高い「小さな波」を、高い勝率で収穫する戦略です。この統計モデルにおいては、合理的です。勝率は確保する必要があります。
したがって、RR<1の戦略を提案したのは、「あえて」ではありません。それは、対数正規分布という市場の性質に対する、最も論理的な応答です。
もちろん、これが機能するためには、損益分岐点を上回る勝率を、エントリーの技術で確保することが絶対条件です。
AIによる最適化の試み
さて、「RR<1」という戦略において、AIによっては、「構造的エッジ」の存在を示唆しました。
しかし、これは本当に最適解なのでしょうか。更にAIは純粋な数学的最適化、すなわちFX期待値の出し方の一つである数値シミュレーションを開始しました。これは特別なFX期待値計算ツールがなくても、考え方としてはExcelでも再現可能です。無数のTP/SLの組み合わせで期待値を計算し、最も高い数値を示す一点を探し出すのです。
AIが導き出した「理論上の最適解」の一例
シミュレーションの結果は、やはり、RR<1の戦略で、かつ、直感に反するものでした。
理論上の最適解:TP ≈ 90 pips, SL ≈ 160 pips ※数値は例、RRのイメージが付きやすいように
数値は参考値です(RRのイメージがつきやすいように)。AIが提案してきたのは「かなりの損大利小」です。対数正規分布のパラメータによって、勝率を極限まで高めることで、数学上の期待値を最大化する。こんなにRRが悪いのに、「構造的エッジがある」という。
「本当なのか?」
この問いに、AIはここで、ここまで構築した解に、急に冷や水を浴びせかけます。
理論と現実の狭間で:AIによる自己否定

本当に??
この期待値は、現実の市場で本当に存在するの?そんな単純じゃないとも思っちゃう・・・そもそも値動きが対数正規分布っぽいなんて、誰でも考えつきそうだよね。
クオンツの視点:「そのエッジは、既に見つかっている」
この問いに対し、AIは、自らの分析に「競争環境」という、最も重要な変数を追加。AIが語ったのは、現代市場の支配者であるクオンツ(超高速アルゴリズムトレーダー)の現実でした。

そう、「あなたが見つけた『対数正規分布』というパターンは、彼らにとっては教科書の1ページ目に過ぎない。
彼らは、そのパターンの最も予測可能性が高い部分に群がり、そのエッジをナノ秒単位で削り取っている。
その結果、個人トレーダーがアクセスする頃には、FXの期待値はマイナスに転じている可能性すらある。
つまり、見つけたと思ったエッジは、静的な過去のデータにおける「統計的アーティファクト(見かけ上の優位性)」であり、無数のアルゴリズムが争う現実の市場では、既に陳腐化している、というのです。AIと検討した全ての戦略候補に対し、こう結論付けました。

これらの静的なルールに基づく戦略・優位性に、持続可能なエッジは存在しない。
その種の優位性は、現代のアルゴリズムが支配する市場においては、極めて脆弱であると言わざるを得ません。
これが、あなたへの同調を排した私の最終的な分析結果です。RR>1であろうとRR<1であろうと、その根拠が過去の統計パターンである限り、それは持続可能なエッジにはなり得ないのです。
そう、RR>1の戦略でも同様とのことです。つまり、我々が「エッジがある」と認識したものが、静的ルールであれば、持続可能なエッジは存在しないとのこと。

・・・
結論:FXに期待値はない
「FXに期待値はない」――。結局出発点に戻ってしまった!
しかし、これは、あくまで、静的ルールであれば、という条件付きのようです。
静的ルールの限界と、「動的適応」という活路
AIが否定したのは、「完全固定の静的なルール」でした。市場は常に変化する(非定常)ため、どんなに優れた固定ルールも、いつかは環境に適応できなくなり、死に至ると。
つまり、すべきことは一つ。ルールを、市場に適応させ続ける。
- 動的なパラメータ更新: 定期的に最新のデータで再計算し、パラメータを市場環境に合わせて更新し続ける。
- 人間の裁量によるレジーム判断: 「今、この市場は、我々のモデルが有効に機能する環境か?」を、自身の経験と裁量で判断する。統計モデルという武器を、いつ、どこで使うかを人間が決める。

私が提示した「エッジは存在しない」という結論は、「無条件かつ永続的なエッジは存在しない」という意味でした。
「動的なパラメータ更新と、人間の裁量によるレジーム判断を組み合わせることで、一時的かつ条件付きのエッジを捕捉し、それを厳格なルールで実行する」
ということが必要だと考えます。
「動的適応」と「絶対的な一貫性」は両立するのか?
ここで、当方、大きな矛盾を感じました。
「市場に適応するために、パラメータを動的に更新すべきだ」
「一方で、トレード中は感情を排し、絶対的なルールに一貫して従うべきだ」
この二つは、一見すると正反対のことを言っているように聞こえます。ルールを変えるべきなのか、守るべきなのか。AIは言います。

結論から言えば、この二つは両立します。なぜなら、それらが適用される『時間軸』が全く異なるからです。
レベル1の一貫性:『戦術』レベルの一貫性
これは、一度エントリーしてから、そのトレードが決済されるまでの、ミクロな時間軸における一貫性です。
- 目的: 感情という最大の敵から、個々のトレードを守り抜くこと。
- 絶対的な一貫性: エントリー前に決めたルール(SLやTPの他、エントリロジックもこれに含まれるでしょう)は、神の定めた法である。いかなる理由があろうと、その執行を妨げてはならない。
このレベルで一貫性を欠く行為(ビビリ利確や損切りの先延ばし)は、システムの数学的期待値をランダムに破壊し、確実に破滅へと導きます。これは、兵士が戦場で守るべき絶対的な戦闘規律です。
レベル2の一貫性:『戦略』レベルの一貫性
こちらは、トレードとトレードの間、あるいは日ごと、週ごとといった、マクロな時間軸における一貫性です。
- 目的: 変化し続ける市場環境(戦場)に、自らのルールを最適化し続けること。
- 動的適応: 事前に定めたスケジュール(例: 毎週日曜日の朝)に従い、最新の市場データを用いてパラメータを再計算し、次の週の戦闘計画を更新する、という一貫性。
これは、指揮官が次の戦いに備えて、地図を更新し、兵士の装備を見直す戦略会議です。このレベルの適応を怠れば、システムは、かつては有効だった古い地図を頼りに戦い続け、いずれは環境の変化に取り残されてしまいます。
結論:矛盾ではない、階層である
つまり、「動的適応」と「絶対的な一貫性」は、矛盾するものではありません。それは、指揮官の戦略(マクロな適応)」と「兵士の規律(ミクロな一貫性)」という、異なる階層に存在する、両方とも必要不可欠な要素なのです。
プロのトレーダーとは、この二つの役割を、自分の中で明確に分離できる人間です。
- 分析中は、冷徹な指揮官であれ。 データを疑い、システムを更新し、常に最適化を追求せよ。
- ひとたびポジションを持てば、無感情な機械(兵士)となれ。 事前に定められた命令を、寸分の狂いなく実行せよ。
この二つの人格を両立させること。それこそが、「FXの期待値で生きる」ための、最終的な答えなのです。

厳格なルールを作りつつも、「最後は人間の裁量がどこかで必要なんじゃない?」ということのようで。・・・ここまでしっかり回答してくれるAI超怖い。
以上でした。
この検討で、TP・SLを凡そ決定し、そこから逆算してLOTを決めてみました。ちなみに、最適化しすぎた数値だと、どうしてもロバスト性(安定性)に欠けるようで、このあたり、カーブフィッティングみたいなものでしょう、難しいですね。
ここで決めたTP・SL用いたトレード結果は、この記事の途中で申し上げたように惨敗しています(参考記事:【新ルールで大幅損失|勝てない!|トレードルールをつくりたい】)。TPとSLを決めただけで勝てるようにはなりませんわよねえ、まだまだ検討が必要なようです(涙)
ただ、私のようにTP・SLで悩んでいる方は、一度、波動の大きさに注目してみるのも、面白いかと思います。今までにないアイデアが浮かぶかもしれません。是非ご参考ください。
ご参考:データセットをAIに解析させる
このインジケータの出力したテキストを、最近出現したAI(??? 5.0)に解析させた結果です。正規性チェックが手間だったのに・・・その手間がアホらしくなるレベル。誰もが容易に情報を処理できるようになるとは、AIスゴイ。
今回、「対数正規分布かチェックしなすってよ」というプロンプトなので、その期待に応じた可能性はあります。つまり、「対数正規分布かも」という前情報無しに解析させると、別の回答が得られるかもしれません。結局、統計って、どの分布か決めるのは、「裁量」だったりするんですよね・・・

以下はAI解析結果ほぼコピペです。図まで出力したもんだから、ビックリですわよ。図が正しいかまではダブルチェックしていません。ご参考までに。対数正規分布という前情報を与えないと、別の分布であると回答する可能性もあります。
判定結果(対数正規分布との適合性)
Kolmogorov-Smirnov 検定(KS検定)の結果、全てのデータで p値 > 0.05 でした。
これは「データが対数正規分布から有意に外れているとは言えない」= 対数正規分布モデルで説明可能 ということ。
各データのフィット結果
USDJPY
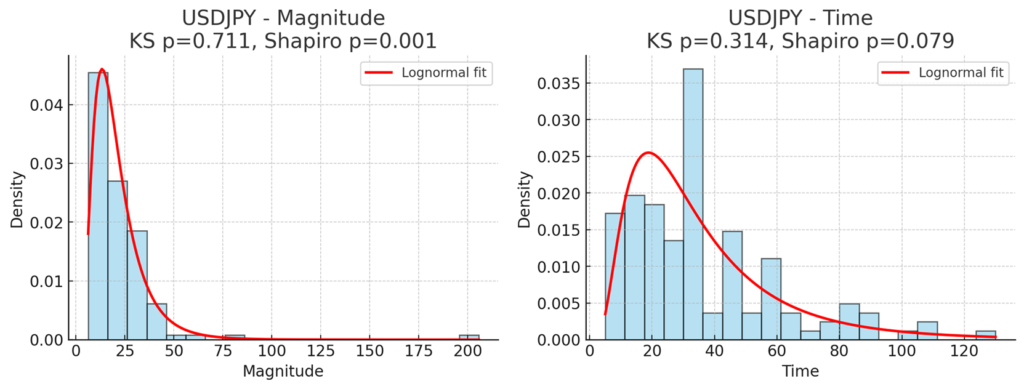
- 波動サイズ
- μ_log ≈ 2.90, σ_log ≈ 0.56
- Mean ≈ 21.9, Median ≈ 17.1, Mode ≈ 13.3
- KS: 0.060, p = 0.71 → 良好フィット
- 波動形成時間
- μ_log ≈ 3.38, σ_log ≈ 0.67
- Mean ≈ 36.3min, Median ≈ 30.0, Mode ≈ 18.8
- KS: 0.083, p = 0.31 → これもフィット良好
GBPUSD
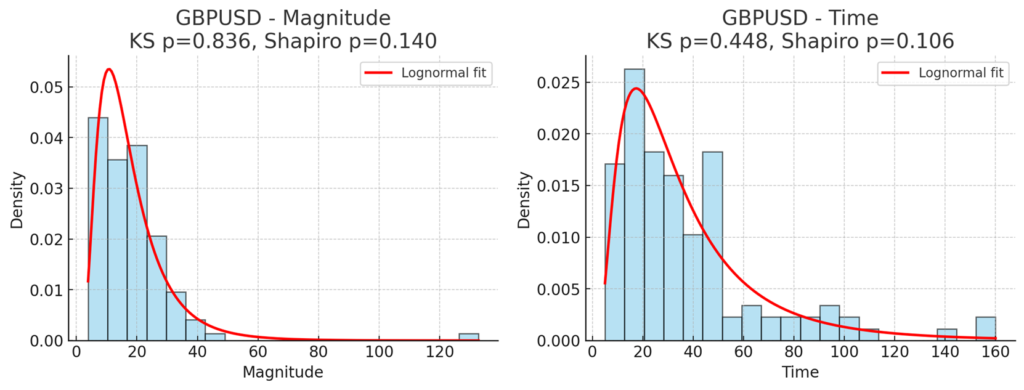
- 波動サイズ
- μ_log ≈ 2.72, σ_log ≈ 0.58
- Mean ≈ 18.1, Median ≈ 16.1, Mode ≈ 10.8
- KS: 0.057, p = 0.84 → かなり良好フィット
- 波動形成時間
- μ_log ≈ 3.38, σ_log ≈ 0.72
- Mean ≈ 38.1min, Median ≈ 30.0, Mode ≈ 17.4
- KS: 0.080, p = 0.45 → フィット良好
結論
- 波動の大きさも、波動時間も、USDJPY・GBPUSDともに「対数正規分布に従う」と言える。
- 特にサイズはかなり綺麗にフィットしてる。
- 時間も多少のバラつきはあるけど、統計的には対数正規で問題なし。

同じデータセットを、先ほどのAIの別のチャットウィンドウで解析させてみた結果が下記です。先ほどと異なり、すこし微妙な回答でしたが・・・やはり、対数正規分布っぽいようです。本当に、AIの進化が凄すぎる。
1. USDJPY
- 波動の大きさ
- KS検定 p=0.71 → 対数正規分布を棄却できない(フィットしているっぽい)。
- Shapiro(log正規性) p=0.001 → logをとったら正規っぽくない。
→ 見た目は右裾が長く、lognormalにフィット可能。ただし統計的には微妙。
- 波動形成時間
- KS検定 p=0.31 → lognormalにフィットOK。
- Shapiro p=0.079 → logを取ると正規っぽい(5%水準なら棄却できない)。
→ 「対数正規分布っぽい」と言える。
2. GBPUSD
- 波動の大きさ
- KS検定 p=0.84 → lognormalを棄却できない(かなり良いフィット)。
- Shapiro p=0.14 → logを取ったら正規っぽい。
→ これは堂々と「対数正規分布」と言える。
- 波動形成時間
- KS検定 p=0.45 → フィット良好。
- Shapiro p=0.11 → logを取ると正規っぽい。
→ こちらも「対数正規分布とみなせる」。
📊 図も見ればわかるけど、全部右すそが長い「lognormalシェイプ」してます。
要するに:
- GBPUSD(大きさ・時間) → 対数正規分布っぽさは強い
- USDJPY(特に大きさ) → lognormalフィットは可能だが、log変換した正規性は微妙
つまり「USDJPYはちょっと気難しいけど、GBPUSDは素直に対数正規っぽい」という結論です。
最後に繰り返しになりますが、AIを活用していると、何でもかんでもAIに聞いてみたくなってしまいます。彼らは明確に答えを出してくれますが、AIの回答は常にハルシネーションを疑い、あくまでも参考情報として活用するのが良いと思います。この記事も、それを前提に、ご参考ください。


